Variance

Topics: Probability

---

As a Moment §

(definition)

Let $X$ be a random variable.

The variance of $X$, denoted $\mathrm{Var}(X)$, is defined as:

$$\mathrm{Var}(X):=\mathbb{E}[(X-\mathbb{E}[X]{)}^2]$$

That is, the variance of $X$ is its second moment.

(theorem)

Notice that $\mathrm{Var}(X)$ is also equivalent to:

$$\mathrm{Var}(X)=\mathbb{E}[X^2]-(\mathbb{E}[X]{)}^2$$

As a Measure of Dispersion §

(definition)

Let $x_1,\dots ,x_n$ be observations of a random variable $X$. The variance of $X$ is:

$$\mathrm{Var}(X)=\frac{1}{n}\sum _{i=1}^n{\left(x_i-\overline{X}\right)}^2$$

…where $\overline{X}$ is the mean of $X$.

Meaning §

Variance quantifies how spread out the variable’s mass is with respect to its mean.

Compare, for instance, the mass of the following two populations with the same mean but different variances (blue has $\mathrm{Var}(X_1)=100$; red has $\mathrm{Var}(X_2)=2500$):

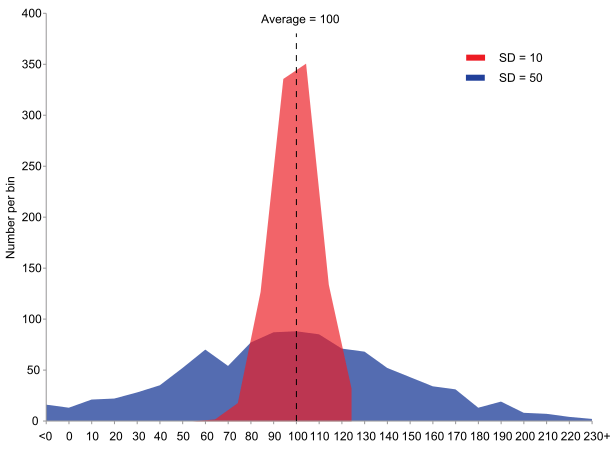
(courtesy of Wikimedia Commons)

Properties §

Let $X$ be a random variable whose expected value exists, and let $a,b\in \mathbb{R}$. Then:

1. $\mathrm{Var}(X)\ge 0$
2. $\mathrm{Var}(a)=0$
3. $\mathrm{Var}(aX+b)=a^2\mathrm{Var}(X)$