Normal Distribution

Topics: Probability - Distribution Function

---

(definition)

Let $X$ be an absolutely continuous random variable.

We say that $X$ has a normal distribution (or Gaussian distribution) if its density function is:

$$f_X(x)=\{\begin{array}{ll}\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}& \text{if }x\in \mathbb{R}\\ 0& \text{otherwise}\end{array}$$

…and write $X\sim \mathcal{N}(\mu ,{\sigma }^2)$.

Applications

Random variables with normal distributions help us model many natural, social and psychological phenomena, including, but not limited to:

• Height
• Effects of a drug
• Intelligence quotient
• Noise level in telecommunications

In particular, the random variable $X$ such that $X\sim \mathcal{N}(0,1)$ is of special importance: its distribution is called the standard normal distribution.

Expected Value and Variance §

Notice that this probability distribution depends on two parameters: $\mu$ and ${\sigma }^2$.

(theorem)

The expected value of an $X$ with a normal distribution is simply and elegantly:

$$\mathbb{E}[X]=\mu$$

(theorem)

The variance of an $X$ with a normal distribution is simply and elegantly:

$$\mathrm{Var}(X)={\sigma }^2$$

Indeed, we use these two values as parameters since:

• $\mu$ provides the value around which most of the mass concentrates. It is a localisation parameter: if we change it, the curve moves horizontally, but it stays otherwise the same.

• $\sigma$ provides the distribution’s standard deviation (i.e. a measure of how disperse the mass is around $\mu$). It is a dispersion parameter: if we change it, the concentration of the mass changes, but the curve stays in the same location.

Examples §

A few examples of the density distribution graphs of various normal distributions with different parameters:

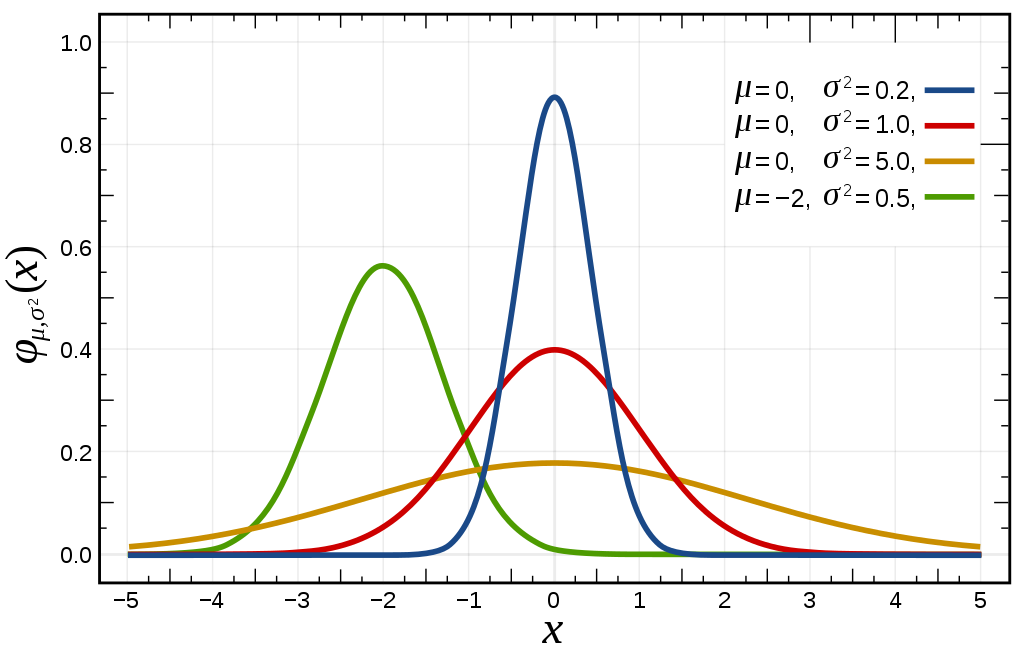
Notice how, effectively, the mass concentrates around $\mu$ and $\sigma$ provides a dispersion measure, as mentioned before.

The red curve is the standard normal distribution.