Derivative of a Vector-Valued Function

Topics: Vector-Valued Function - Calculus

---

(definition)

Let $r(t):\mathbb{R}\to {\mathbb{R}}^n$ be a vector-valued function.

The derivative $r^{\prime }(t)$ of $r(t)$ is defined by:

$$r^{\prime }(t):=\underset{\Delta t\to 0}{\lim }\frac{r(t+\Delta t)-r(t)}{\Delta t}$$

…for any values of $t$ for which the limit exists. When the limit as $t\to a$ exists, we say that $r$ is differentiable at $t=a$.

We can also derivate operated vector-valued functions.

Division

The division in this definition is symbolic. As we can’t divide vectors, It means the scalar multiplication of $r(t+\Delta t)-r(t)$ by $\frac{1}{\Delta t}$.

(theorem)

If we develop the limit given in this definition, we’ll find that, if $r(t)=(r_1(t),r_2(t),\dots ,r_n(t))$, then:

$$r^{\prime }(t)=⟨r_1^{\prime }(t),r_2^{\prime }(t),\dots ,r_n^{\prime }(t)⟩$$

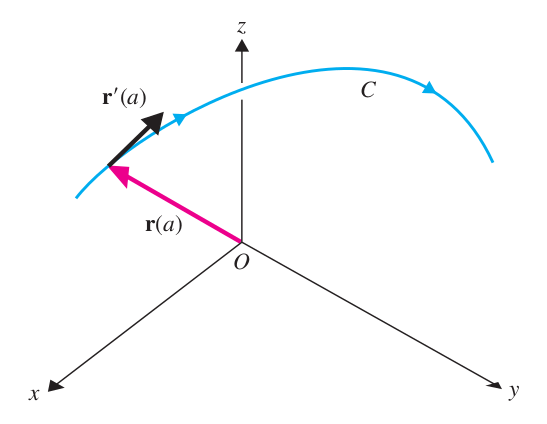
Graphical Representation §

Graphically, the derivative of a vector-valued function is the tangent vector to the function’s curve at $t=a$.