Bisection Method

Topics: Numerical Analysis

---

The bisection method is a closed numerical method that can solve equations (i.e. find the zeroes (roots) of the associated function).

As it name implies, to find a given zero, this method bisects a given interval in the function.

Procedure §

Let $f(x)$ be any continuous function defined in an interval $[a,b]$, with $f(a)$ and $f(b)$ having different signs. Then, there exists a $p$, $a<p<b$, such that $f(p)=0$:

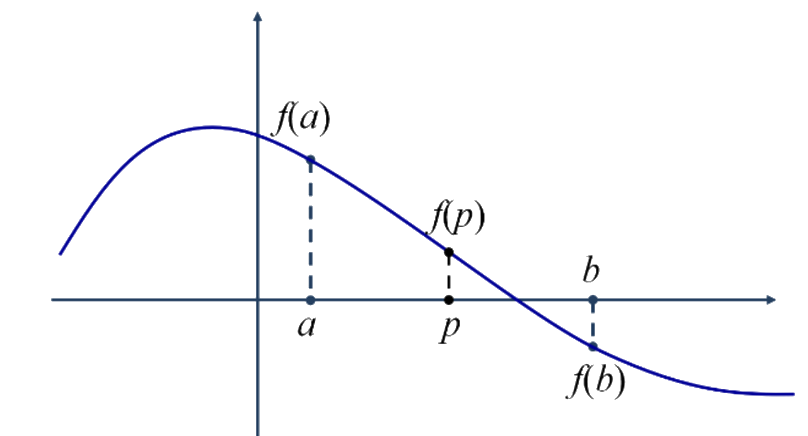
To find $p$, we follow these steps:

1. We choose an initial interval $[a,b]$
2. To guarantee that the interval contains a root, we verify that $f(a)f(b)<0$
3. We calculate the middle point of this interval: $p=\frac{b-a}{2}$
4. We verify that $|f(p)|<\xi$, where $\xi$ is the tolerated solution interval. If this is true, then the process is done. If it is not, then we continue with the next step
5. We locate the half that contains the root and we reassign the interval:
   • If $f(a)f(p)<0$, then $b\leftarrow p$ (i.e. our new $b$ will be $p$)
   • If not, then $a\leftarrow p$
6. We redivide the interval (step 3 and onward)

Considerations §

Solution and Approximation §

This method finds the root when $f(p)=0$. However, this method only yields an approximation, so it is necessary to determine a margin of tolerance (this is what we called $\xi$ in the previous steps).

Also note that this method finds only one root out of all the possible roots of the equation.

When to Stop §

We can stop this method when we have reached a root that’s within the margin of error. However, we can also stop this method after a certain number of iterations.

With an error margin $\xi >0$, $N$ the number of iterations carried out, and $p_N$ the last approximation, we can stop the method when any of the following becomes true, according to our needs:

$$|f(p_{N)}|<\xi$$

$$|p_N-p_{N-1}|<\xi$$

$$\frac{|p_N-p_{N-1}|}{|p_N|}<\xi ,p_N\ne 0$$

Advantages and Disadvantages §

Advantages:

• It always converges to a solution
• It’s used as an initial part of other more efficient methods
• It’s easy to program
• The final interval serves as an error bound

Disadvantages:

• It converges slowly
• If the interval doesn’t contain a root, the method will approximate to the original limits
• If the interval contains more than one solution, it could find any of them, or reach a value that is not a root

Convergence §

(theorem)

Let $f\in [a,b]$ and suppose that $f(a)f(b)<0$. The bisection method generates a sequence $\{p_N\}$ that approximates $p$ with the property:

$$|p_N-p_{N-1}|\le \frac{b-a}{2^n}$$

…given $N\ge 1$. Notice that this property is basically the error bound we mentioned earlier in the advantages of the method.

Example

We can use this theorem to determine the number of iterations we need to approximate a root within a certain margin of error.

For example, let’s find a root for $x^3+x^2+4x-1=0$ in the interval $[1,2]$.

We start by isolating $N$:

$$|p_N-p_{N-1}|\le \frac{b-a}{2^n}$$

$$|p_N-p_{N-1}\le 2^{-N}(b-a)\le 10^{-5}$$

$$|p_N-p_{N-1}|\le 2^{-N}\le 10^{-5}$$

$$2^{-N}\le 10^{-5}$$

…then by calculating the base 10 logarithm on both sides:

$${\log }_{10}(2^{-N})\le {\log }_{10}(10^{-5})$$

$$-N{\log }_{10}(2)\le -5$$

$$N\ge \frac{5}{{\log }_{10}(2)}\approx 16.609$$

Thus, we need approximately 17 iterations to reach the desired precision.