False Position Method

Topics: Numerical Analysis

---

The false position method is a closed numerical method that tries to find the zeroes of a given function. This method is similar to the bisection method, with the only difference between them being the way we choose the middle point.

Procedure §

To use this method, we first suppose that a zero of the function is between any two initial points $x_0$ and $x_1$, chosen such that $f(x_0)$ and $f(x_1)$ are of opposite signs.

Next, we draw a line from $f(x_0)$ to $f(x_1)$, and we call $x_2$ its intersection with the $x$ axis. In the same way we do for the bisection method, we will use $x_2$ and its relation to $x_0$ and $x_1$ to continue finding an approximation to the zero of the function.

That is, for the iterations that follow, if $f(x_2)$ and $f(x_0)$ have opposite signs, then we’ll set $x_1=x_2$; if not, then we’ll set $x_0=x_2$.

How to find $x_2$

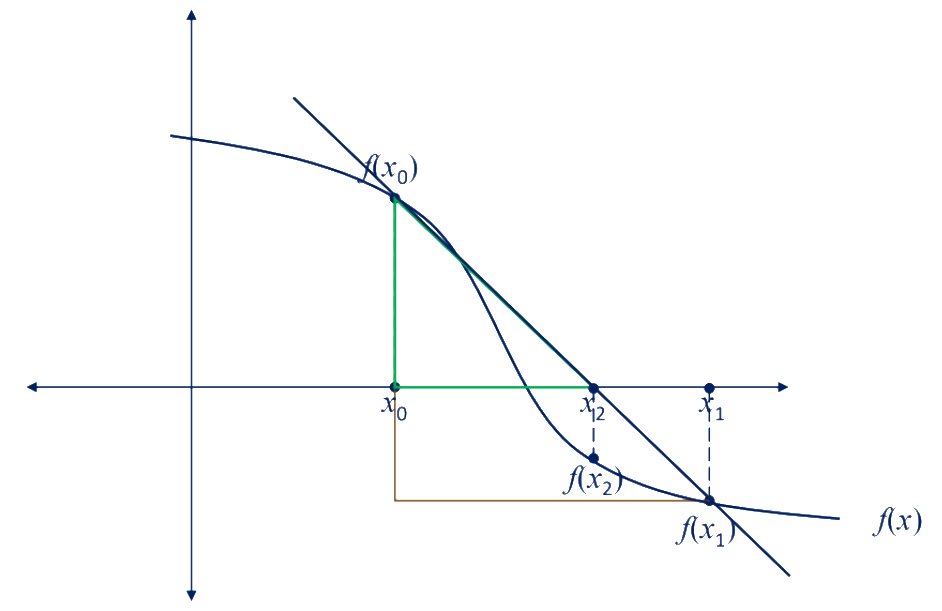
Let’s first visualise the procedure for this method:

Notice that, with the help of the green and brown triangle in the above image, we can tell that:

$$\frac{x_2-x_0}{f(x_0)}=\frac{x_1-x_0}{f(x_0)-f(x_1)}$$

…so by isolating $x_2$, we get:

$$x_2=x_1-f(x_1)\frac{x_0-x_1}{f(x_0)-f(x_1)}$$

Similarities with the Bisection Method §

Approximation and Stopping §

Since this method works similarly to the bisection method, it also yields just an approximation to the real value, so we have to define a margin of tolerance before starting.

In the same way, we can use the same conditions we used for the bisection method for stopping this method.

Advantages and Disadvantages §

The false position method has almost the same advantages and disadvantages as the bisection method, except for the fact that:

• Advantage: This method converges faster
• Disadvantage: The final interval is not always useful as an error bound