Havel-Hakimi Algorithm

Topics: Graph Theory

---

The Havel-Hakimi algorithm is an algorithm that lets us know if there exists a simple graph whose degree sequence is a given non-increasing sequence of non-negative integers.

The algorithm consists of the following steps:

1. Take the first greatest integer. Let $n$ be this value.
2. Remove $n$ from the sequence
3. Subtract $1$ from the next $n$ integers.
4. Reorder the sequence so that it is non-increasing again.
5. Repeat steps 1 through 4 until we reach a sequence that consists of all zeroes or we get a negative integer.

When the resulting sequence consists of all zeroes, the sequence corresponds to a simple graph and we say that it is a graphic sequence. Otherwise, the sequence doesn’t correspond to a simple graph and we say that it is non-graphic.

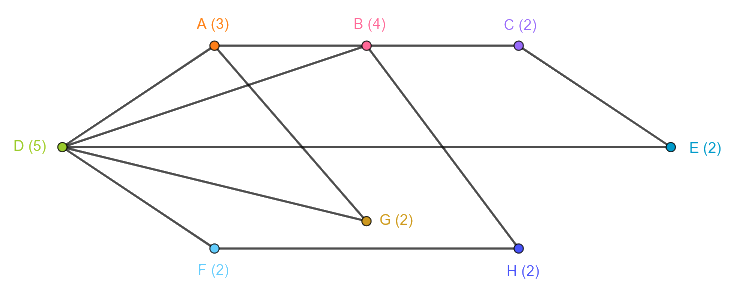
Graphic Example

Let $\{5,4,3,2,2,2,2,2\}$ be our sequence. By following the algorithm, we get:

1. First iteration:
2. $n=5$
3. $\{\cancel{5},4,3,2,2,2,2,2\}$
4. $\{3,2,1,1,1,2,2\}$
5. $\{3,2,2,2,1,1,1\}$
6. Second iteration:
7. $n=3$
8. $\{\cancel{3},2,2,2,1,1,1\}$
9. $\{1,1,1,1,1,1\}$
10. $\{1,1,1,1,1,1\}$
11. Third iteration:
12. $n=1$
13. $\{\cancel{1},1,1,1,1,1\}$
14. $\{0,1,1,1,1\}$
15. $\{1,1,1,1,0\}$
16. Fourth iteration:
17. $n=1$
18. $\{\cancel{1},1,1,1,0\}$
19. $\{0,1,1,0\}$
20. $\{1,1,0,0\}$
21. Fifth iteration:
22. $n=1$
23. $\{\cancel{1},1,0,0\}$
24. $\{0,0,0\}$
25. $\{0,0,0\}$

Voilà. Since the resulting sequence consists of all zeroes, the sequence is graphic. In effect, its associated simple graph is the following: